Inclined Fire, part #3.5: Even Better Rifleman's Rule
Here it comes.
EBRR?
or
Increasingly Improved Rifleman's Rule = IIRR? 2I2R = two-eye-two-arr?Naming contest is still ongoing, suggestions are welcome.
When analyzing errors of Improved Rifleman's Rule (which appeared the most promising), I noticed that they are more or less (well enough for a heuristic method) linear in distance, at least for angles beyond ±20º.
GP11 Improved Rifleman's Rule errors, 0.1 mrad clicks
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
| 300 | 0.36 | 0.62 | 0.99 | 1.44 | 1.95 | 2.55 | 3.19 | 3.94 | 4.71 | 8.16 |
| 400 | 0.35 | 0.64 | 1.01 | 1.46 | 1.98 | 2.60 | 3.28 | 4.01 | 4.80 | 8.28 |
| 500 | 0.31 | 0.59 | 0.96 | 1.42 | 1.95 | 2.57 | 3.25 | 4.02 | 4.83 | 8.46 |
| 600 | 0.27 | 0.54 | 0.90 | 1.36 | 1.88 | 2.50 | 3.20 | 3.98 | 4.80 | 8.54 |
| 700 | 0.21 | 0.48 | 0.82 | 1.26 | 1.79 | 2.42 | 3.12 | 3.88 | 4.74 | 8.58 |
| 800 | 0.14 | 0.38 | 0.72 | 1.14 | 1.67 | 2.28 | 2.99 | 3.78 | 4.63 | 8.61 |
| 900 | 0.06 | 0.26 | 0.58 | 1.00 | 1.50 | 2.11 | 2.82 | 3.61 | 4.48 | 8.65 |
| 1000 | -0.07 | 0.11 | 0.39 | 0.79 | 1.29 | 1.88 | 2.59 | 3.38 | 4.27 | 8.66 |
| 0.20 | 0.45 | 0.80 | 1.23 | 1.75 | 2.36 | 3.05 | 3.82 | 4.66 | 8.49 | |
| -15 | -20 | -25 | -30 | -35 | -40 | -45 | -50 | -55 | -60 | |
| 300 | 0.39 | 0.68 | 1.09 | 1.51 | 2.05 | 2.62 | 3.29 | 4.01 | 4.77 | 8.07 |
| 400 | 0.45 | 0.77 | 1.16 | 1.61 | 2.15 | 2.77 | 3.45 | 4.18 | 4.95 | 8.32 |
| 500 | 0.49 | 0.81 | 1.22 | 1.70 | 2.25 | 2.89 | 3.57 | 4.30 | 5.11 | 8.50 |
| 600 | 0.52 | 0.88 | 1.30 | 1.79 | 2.35 | 2.98 | 3.68 | 4.43 | 5.24 | 8.63 |
| 700 | 0.59 | 0.95 | 1.38 | 1.90 | 2.48 | 3.12 | 3.82 | 4.57 | 5.37 | 8.74 |
| 800 | 0.67 | 1.05 | 1.51 | 2.04 | 2.62 | 3.28 | 3.98 | 4.74 | 5.53 | 8.84 |
| 900 | 0.76 | 1.16 | 1.65 | 2.20 | 2.80 | 3.46 | 4.17 | 4.92 | 5.70 | 8.92 |
| 1000 | 0.87 | 1.31 | 1.82 | 2.40 | 3.02 | 3.68 | 4.40 | 5.14 | 5.92 | 9.05 |
| 0.59 | 0.95 | 1.39 | 1.89 | 2.47 | 3.10 | 3.80 | 4.54 | 5.32 | 8.63 |
The takeaway is that at a given angle errors are approximately proportional to distance, therefore correction in clicks will depend only on the inclination. This is good news.
Now how they depend on the inclination -- that is the question. Let's take average correction in clicks for a given angle (green cells at the bottom), and get a robot to draw us a nice picture.
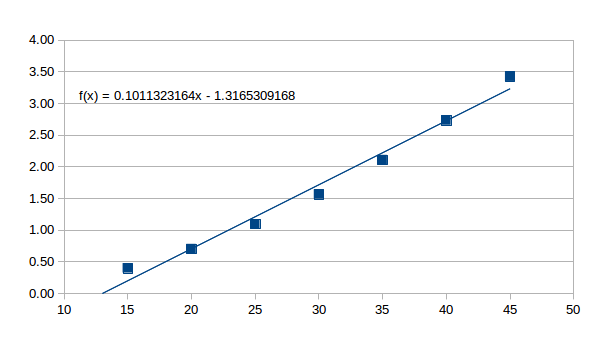
Jackpot!
The straight line is linear regression. (For the nerdy types, like me -- I know it is not linear strictly speaking, but it is linear enough for a heuristic method). In regression formula above, slope is saying "1 click per each 10 degrees", while intercept is saying "starting from 20 degrees". Residuals remain within ± half a click.
The algorithm is simple (this, my friend, is the actual EBRR (or was it 2I2R?)):
1. Calculate correction as per Improved Rifleman's Rule;
2. Subtract from the result 1 click per each 10 degrees above 10:
20º minus 1 click
30º minus 2 clicks
40º minus 3 clicks
etc.
GP11 2I2R (or was it EBRR?) vertical miss distance, cm
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
| 300 | 1.1 | -1.2 | 0.0 | -1.9 | -0.2 | -1.7 | 0.8 | -0.3 | 3.7 | 3.2 |
| 400 | 1.4 | -1.5 | 0.0 | -2.5 | -0.1 | -2.1 | 1.6 | 0.1 | 5.6 | 5.2 |
| 500 | 1.6 | -2.2 | -0.2 | -3.4 | -0.3 | -2.8 | 1.8 | 0.1 | 7.2 | 7.0 |
| 600 | 1.7 | -2.9 | -0.7 | -4.4 | -0.9 | -3.9 | 1.7 | -0.2 | 8.4 | 8.3 |
| 700 | 1.5 | -3.9 | -1.4 | -6.0 | -1.8 | -5.3 | 1.2 | -1.3 | 9.0 | 9.0 |
| 800 | 1.2 | -5.3 | -2.5 | -7.9 | -3.2 | -7.5 | -0.1 | -2.8 | 8.8 | 8.9 |
| 900 | 0.5 | -7.0 | -4.2 | -10.4 | -5.5 | -10.4 | -2.3 | -5.4 | 7.6 | 7.8 |
| 1000 | -0.7 | -9.4 | -6.7 | -14.0 | -8.7 | -14.6 | -5.9 | -9.6 | 4.7 | 4.8 |
| -15 | -20 | -25 | -30 | -35 | -40 | -45 | -50 | -55 | -60 | |
| 300 | 1.2 | -1.0 | 0.3 | -1.7 | 0.2 | -1.5 | 1.2 | 0.0 | 4.0 | 3.4 |
| 400 | 1.9 | -1.0 | 0.7 | -1.8 | 0.8 | -1.2 | 2.6 | 1.1 | 6.6 | 6.4 |
| 500 | 2.5 | -1.0 | 1.2 | -1.7 | 1.5 | -0.7 | 4.0 | 2.3 | 9.6 | 9.4 |
| 600 | 3.2 | -0.8 | 2.0 | -1.4 | 2.6 | -0.1 | 5.8 | 4.0 | 12.9 | 12.9 |
| 700 | 4.2 | -0.4 | 2.9 | -0.8 | 4.1 | 1.1 | 8.1 | 6.2 | 16.7 | 17.0 |
| 800 | 5.5 | 0.4 | 4.5 | 0.4 | 6.1 | 2.9 | 11.1 | 9.2 | 21.4 | 21.7 |
| 900 | 7.1 | 1.6 | 6.5 | 2.0 | 8.8 | 5.4 | 14.9 | 12.9 | 26.7 | 27.4 |
| 1000 | 9.0 | 3.3 | 9.1 | 4.6 | 12.4 | 8.9 | 19.7 | 17.7 | 33.5 | 34.4 |
Hooray, comrades. The lawn looks sufficiently green and no longer undermines property value.
Let's check elsewhere.
GP90 errors, clicks
(A reminder to our foreign friends, GP90 is the standard Swiss military issue of 5.56×45mm NATO.)
GP90 Even Better Rifleman's Rule vertical miss distance, cm
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
| 300 | 1.1 | -1.1 | 0.1 | -1.8 | 0.0 | -1.7 | 1.1 | -0.1 | 3.9 | 3.3 |
| 400 | 1.6 | -1.4 | 0.4 | -2.1 | 0.4 | -1.4 | 2.3 | 1.0 | 6.7 | 6.7 |
| 500 | 2.0 | -1.6 | 0.5 | -2.4 | 0.9 | -1.5 | 3.5 | 2.1 | 9.6 | 10.1 |
| 600 | 2.3 | -2.0 | 0.6 | -2.8 | 1.2 | -1.4 | 4.6 | 3.1 | 12.5 | 13.3 |
| 700 | 2.9 | -2.1 | 1.0 | -3.1 | 1.7 | -1.2 | 6.0 | 4.4 | 15.7 | 16.9 |
| 800 | 3.3 | -2.4 | 1.2 | -3.3 | 2.2 | -1.0 | 7.2 | 5.7 | 18.7 | 20.6 |
| 900 | 3.2 | -3.4 | 0.4 | -4.8 | 1.3 | -2.5 | 7.0 | 5.2 | 19.9 | 22.1 |
| 1000 | 1.3 | -6.6 | -3.1 | -9.4 | -3.1 | -7.8 | 2.2 | 0.0 | 16.1 | 18.5 |
| -15 | -20 | -25 | -30 | -35 | -40 | -45 | -50 | -55 | -60 | |
| 300 | 1.3 | -1.0 | 0.3 | -1.7 | 0.1 | -1.5 | 1.1 | -0.1 | 3.9 | 3.3 |
| 400 | 1.7 | -1.1 | 0.6 | -1.9 | 0.7 | -1.2 | 2.6 | 1.3 | 7.1 | 6.9 |
| 500 | 2.2 | -1.3 | 0.9 | -2.0 | 1.3 | -1.0 | 4.1 | 2.6 | 10.1 | 10.5 |
| 600 | 2.8 | -1.5 | 1.3 | -2.1 | 1.9 | -0.7 | 5.4 | 4.0 | 13.2 | 13.9 |
| 700 | 3.3 | -1.6 | 1.7 | -2.3 | 2.5 | -0.4 | 6.7 | 5.1 | 16.2 | 17.1 |
| 800 | 3.7 | -1.8 | 1.8 | -2.6 | 2.9 | -0.4 | 7.9 | 6.1 | 18.9 | 20.2 |
| 900 | 4.9 | -1.1 | 3.3 | -1.5 | 5.0 | 1.5 | 11.1 | 9.4 | 23.9 | 25.7 |
| 1000 | 7.7 | 1.7 | 7.2 | 2.5 | 10.4 | 7.2 | 18.4 | 16.9 | 33.7 | 36.1 |
I'm sure you always wanted to shoot Fass 90 at 1,000 m and 50 degree inclination.
Now you can do it with a 0.029 cm accuracy.
.338 Lapua Magnum errors, clicks

.338 LM Even Better Rifleman's Rule vertical miss distance, cm
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
| 300 | 0.9 | -1.5 | -0.6 | -2.8 | -1.5 | -3.7 | -1.7 | -3.9 | -1.1 | -3.5 |
| 400 | 1.2 | -2.1 | -0.7 | -3.7 | -1.9 | -4.6 | -1.9 | -4.7 | -0.7 | -3.3 |
| 500 | 1.5 | -2.5 | -0.9 | -4.6 | -2.2 | -5.6 | -2.1 | -5.4 | -0.3 | -3.3 |
| 600 | 1.7 | -3.1 | -1.2 | -5.6 | -2.6 | -6.7 | -2.6 | -6.3 | -0.1 | -3.6 |
| 700 | 1.8 | -3.8 | -1.6 | -6.8 | -3.4 | -8.0 | -3.1 | -7.5 | -0.2 | -4.1 |
| 800 | 2.0 | -4.5 | -2.0 | -7.9 | -4.1 | -9.5 | -3.8 | -8.8 | -0.1 | -4.5 |
| 900 | 2.1 | -5.4 | -2.6 | -9.2 | -4.9 | -10.9 | -4.6 | -10.2 | -0.5 | -5.2 |
| 1000 | 2.0 | -6.3 | -3.2 | -10.7 | -5.9 | -12.8 | -5.6 | -11.8 | -1.0 | -6.1 |
| -15 | -20 | -25 | -30 | -35 | -40 | -45 | -50 | -55 | -60 | |
| 300 | 1.0 | -1.4 | -0.5 | -2.7 | -1.4 | -3.6 | -1.6 | -3.7 | -1.0 | -3.3 |
| 400 | 1.4 | -1.7 | -0.5 | -3.3 | -1.5 | -4.2 | -1.5 | -4.2 | -0.2 | -2.9 |
| 500 | 1.8 | -2.0 | -0.4 | -3.9 | -1.4 | -4.7 | -1.3 | -4.4 | 0.6 | -2.5 |
| 600 | 2.3 | -2.2 | -0.2 | -4.3 | -1.3 | -5.2 | -0.9 | -4.6 | 1.7 | -1.8 |
| 700 | 2.8 | -2.5 | 0.0 | -4.8 | -1.1 | -5.6 | -0.5 | -4.7 | 2.7 | -1.1 |
| 800 | 3.5 | -2.5 | 0.4 | -5.0 | -0.7 | -5.7 | 0.3 | -4.6 | 4.0 | -0.1 |
| 900 | 4.3 | -2.5 | 1.0 | -5.1 | -0.3 | -5.8 | 1.0 | -4.3 | 5.6 | 0.8 |
| 1000 | 4.9 | -2.5 | 1.3 | -5.2 | 0.2 | -6.0 | 1.8 | -4.0 | 7.0 | 1.9 |
.338 is already convincing enough on flatlands. In the mountains, combined with 2I2R, this is downright WMD and total nuke from the orbit.
Let's recap: we found a simple heuristic that can use existing ballistic tables and has excellent accuracy with various calibers.
Yet it has two limitations:
1. Only works with 100 m zero;
2. Only works with 0.1 mrad clicks.
Well, it works with MOA or other clicks, just not as simple to remember (for example, 300 m zero calls for 0.1 MILs per 5 degrees over 10).
Full algorithm:
1. Measure the inclination α;
2. Measure the slant distance (along LOS) D;
3. Look up bullet path (come-up) in ballistic table as if shooting at distance D horizontally;
4. Multiply this correction (and not distance D) by cos(α).
5. Subtract one click per each ten degrees of inclination over ten, i.e., 20º -1 click, 30º -2 clicks, 40º -3 clicks, etc.
6. Profit!
Accuracy: A;
Domain: all practical angles, distances, and calibers.
Complexity: low -- 1 table lookup, 1.5 mathematical operations.
Pros: accuracy, simplicity.
Cons: only works with 100 m zero and 0.1 MIL clicks