Before jumping into formulas it makes sense to get an intuitive understanding of forces at work. School-level knowledge of Newton's laws of motion and basic trigonometry will suffice.

Bullet Trajectory

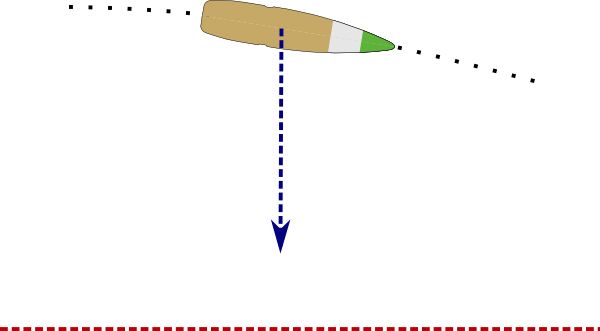
The black dashed line on the picture above shows trajectory of a .50 cal armor-piercing incendiary bullet. Red line of sight (LOS) goes straight from shooter's eye to the target. We are primarily interested in distances between trajectory and LOS, because that's what we'll compensate with scope's elevation turret.

Blue arrow shows vector of gravity acting on the bullet. By the time my favorite GP11 bullet reaches 800 meters, it drops 7 meters below line of sight (throughout this document I will assume 100 meter zero).

Here's how things change when shooting at an upward angle:

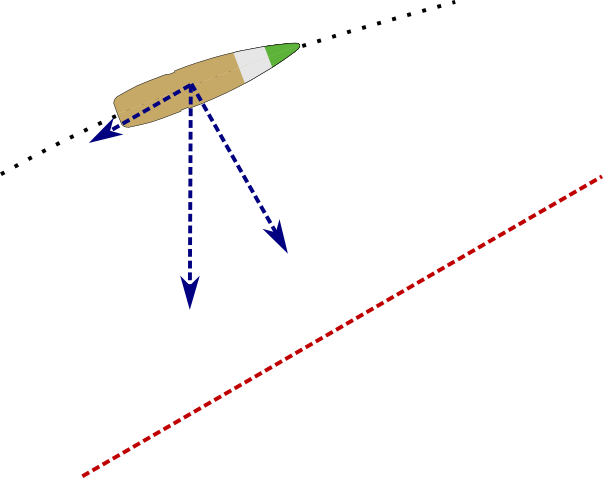
Exact same gravity is still pulling down, but "down" is no longer "perpendicular to LOS". Only one component of gravity is bending trajectory towards LOS, the perpendicular one. Which means that bullet flies higher than when shooting horizontally.

Side note: the other component does act to slow the bullet down, but given typical speed of modern rifle bullets the effect is barely noticeable.

Opposite scenario - this time we're high on the hill, shooting down.

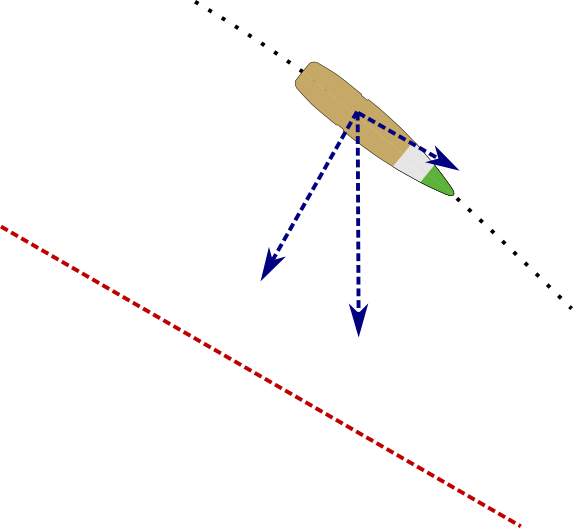
The logic is the same - only the perpendicular component of gravity is bending bullet trajectory towards LOS, therefore bullet flies higher than when shooting horizontally.

Replay: when shooting at an angle, no matter if it's up or down, bullet goes higher than when shooting horizontally. Given the same angle, depressed fire trajectory is slightly higher than elevated one, but the difference is so small it can be ignored at most practical distances.

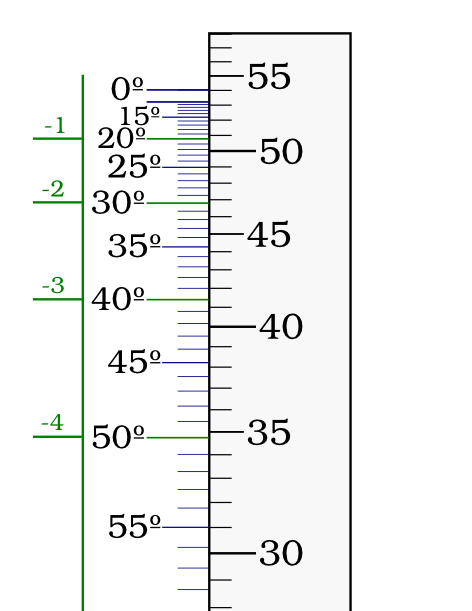
How much is 1 MIL

Let's say your scope has MIL turrets (one click is 0.1 MIL), and you are asked "how much is 1 click at 500 m". You'd be inclined to say "5 cm" - but that's not the right answer, at least as far as inclined fire is concerned.

Let's start with a simple horizontal example:

We changed our aim by a small angle r when shooting at distance D. (Picture is not to scale; in reality 0.1 MIL ≃ 0.00573 degrees.) Corresponding change in heigh would be

d = D * tan(r)

Remember SohCahToa? That's toa, or Tangent = Opposite / Adjacent. For small angles r expressed in radians tan(r) ≃ r. For example, one click is 0.1 MIL, which is 0.0001 radians, and tan(0.0001) = 0.000100000000333... (very close to 0.0001).

So if r is in MILs, then d ≃ D * r / 1000.

Now back to our hills.

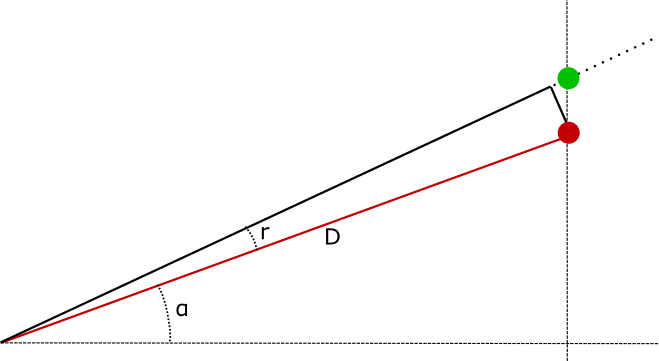
The whole thing is now rotated by angle α, which is much bigger than r and convenient
approximation no longer holds.

Zooming in:

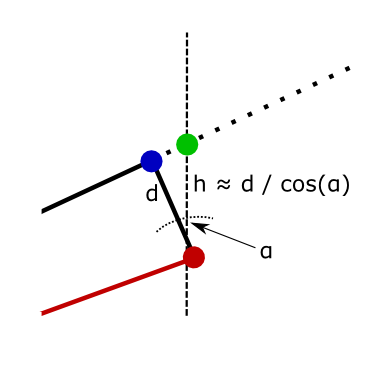
It's not like d is now different. It's the same distance, perpendicular to LOS, but just no longer vertical. The "true" vertical distance, perpendicular to the Earth surface is h = d / cos(α). One click in the mountains is taller than one click in the flatlands. For example, if α = 30º one click raises point of impact 15% more. You need to keep that in mind when correcting vertical miss (and divide clicks by cosine). Better yet do all math in MILs (or other angular units) rather than meters (or other length units). Another point to MIL/MIL scopes.

Last point here: all ballistic calculators I have seen so far measure bullet path in direction perpendicular to LOS, not in vertical direction.

Ballistic calculators

This subject requires a separate article (what makes ballistic calculator good, why in practice there is a difference between theory and practice, etc.) For now I'll keep it short:

1. Use a good ballistic calc:
1.1. Bryan Litz's excellent http://appliedballisticsllc.com/ calculator
https://play.google.com/store/apps/details?id=com.appliedballisticsllc.a...
1.2. http://www.jbmballistics.com/
(also good, convenient interface, intelligent tech support)
2. Calculator has to support G7 model. G1 does not fit modern bullets at speeds approaching the speed of sound (starting roughly at Mach 1.2), and sometimes even closer than that.
3. Calculator should show different adjustments for angles of same magnitude but opposite signs (up vs. down).
4. If possible, calculator should take into consideration air density change with altitude.
(Pts. 3 and 4 are a reasonable indication that the solver correctly predicts trajectory with inclined line of sight.)

Subjective inclination

After handing a rifle with Angle Cosine Indicator (ACI), I was surprised at how far perceived angle is from reality.

Reality: 30º
Perception: really steep angle, "maybe 45 degrees"

Reality: 45º
Perception: "barrel points to the sky, approximately 60 degrees"

Reality: 60º
Perception: "nearly straight up"

Talking to more experienced shooters provided confirmation: yep, that's the way it is, especially hunters are known to brag about "a goat at 800 m 45º up".

But play a bit with ACI (or even school protractor with a piece of string attached) and illusion quickly goes away.

Data parameters and colours

The tables that follow are based on data from JBM ballistic calculator
http://www.jbmballistics.com/cgi-bin/jbmtraj_simp-5.1.cgi ("simplified" version)
with the following parameters:

Environment
Pressure: 1014 hPa
Temperature: 15 ºС
Humidity: 76%

I probably should have used 1000/15/50 common in Soviet manuals or 955/15/55 like in Swiss manuals, but what's done is done. Besides, it doesn't matter much.

Calibers:

GP90 5.56x45 -- bullet weight 4.1 g, caliber 5.56 mm, BC G7 0.167, V0 905 m/s, sight height 7 cm. (for our foreign friends -- this is Swiss army ordnance issue of 5.56x45 NATO)
GP11 7.5x55 -- bullet weight 174 gr, caliber 7.62 mm, BC G7 0.278, V0 780 m/s, sight height 4 cm. (for our foreign friends -- the ballistics are very close to a good .308)
.338 Lapua Magnum 8.6x70 -- bullet weight 250 gr, caliber 8.61 мм, BC G7 0.322, V0 905 m/s, sight height 4 cm.

All zeroed at 100 m unless explicitly stated otherwise. Distances in meters, angles in degrees, drops and bullet paths in centimetres.

Positive path values mean that bullet is above LOS.

Cell colouring is based on torso target size.

Now let's see when inclination does matter.

The table below shows what happens when slope is ignored, i.e. there is no correction for inclination. (Errors in cm, same color coding as above).

GP11 vertical miss distance, cm

Middle distances look abysmal for all but very mild inclination angles and appear to require ballistic calculator, precomputed tables, or at least some heuristic better than "aim low".

There are several such heuristics. The three most popular are Rifleman's rule, improved rifleman's rule, and Sierra's:
http://www.exteriorballistics.com/ebexplained/article1.html

The fourth method is taught by NDS, and fifth is described later in this series.

Moving on to the most popular empirical method - Rifleman's rule.

The idea is very simple:

1. Measure inclination α;
2. Measure distance to target D (along line of sight);
3. Calculate equivalent horizontal distance De = D * cos(α);
4. Look up compensation as if shooting horizontally at distance De.

Rifleman's rule has another nice property besides simplicity: it does not depend on the rifle, caliber, zero distance, etc. - just inclination and distance. This allows implementing it in universal laser rangefinders.

Sadly it is based on the assumption that bullet travels in vacuum (space marines, nota bene), and its use on Earth has significant limitation.

GP11 vertical miss distance, cm

Bottom line: rifleman's rule is better than nothing and better than NDS "method". Yet 600 m at 30º is well in the red, explaining longevity of paper plate mentioned at the beginning of this article.

But why is everybody using rifleman's rule then? The answer is mostly hidden just outside of the table. Rifleman's rule works fine at distances shorter than 300 m, and is acceptable up to 400 m, which covers the majority of hunting applications. Army sniping relies on hunting skills, both historically (as the name implies) and currently (hunting experience is still a plus for an army sniper). But the table shows that what works for hunting in the mountains does not work well for game that shoots back, requiring you to keep the distance.

Rifleman's rule consistently overestimates the effect of inclination for the three calibers that I looked at. After using this method, impacts are below the target. Predictability is good, one can come up with an empirical rule like "for inclinations above x degrees at y meters, aim at shoulder level". Yet for reasons explained later in this article I decided not to bother.

Accuracy: acceptable
Domain: 30º, 500 m. Maybe a little more if holding a correction.
Complexity: very simple -- 1 table lookup, 1 mathematical operation, often automated.
Pros: beautiful simplicity, independence from rifle and caliber, no need to amend or extend existing ballistic tables.
Cons: surprisingly limited applicability.

But not to despair, there's hope. Read on.

Now we proceed to the most accurate approximate method used by Sierra Bullets. Only proper ballistic calculator can do better.

But there's no free lunch - we'll need information not normally found in ballistic tables, namely vertical bullet drop at various distances. See the following picture for explanation.

As before, red line (LOS) goes straight from shooter's eye to target. Green line is bore axis.

Blue arrow d is bullet path, perpendicular to LOS. Coyote brown arrow d' is vertical drop. In absence of gravity, the bullet would continue along bore axis and drop would remain zero. On Earth drop is zero at the muzzle and negative throughout the rest of trajectory -- that is, below the bore axis. Bullet path, on the other hand, can be either positive or negative (above or below the LOS).

To calculate drop table in JBM, set sight height to 0 and zero distance to 1 m.

Sierra's correction is calculated as follows:

1. Measure inclination α;
2. Measure the slant distance (along LOS) D;
3. Look up in regular ballistic table bullet path d that corresponds to distance D;
4. Look up in drop table drop d' that corresponds to distance D and flip its sign;
5. Sierra's correction = d + (1 - cos(α)) * d'

Impressive results:

GP11 vertical miss distance, cm

Terrific, isn't it?

Bottom line:

Accuracy: A+!
Domain: as far as the eye can see
Complexity: complex! 2 table lookups, 3 mathematical operations
Pros: accuracy is as good as it gets
Cons: too complex to be useful, requires extra data (regular ballistic tables are not enough)

Shooting rules of thumb should work under stress. Sierra method is too complex to be of much use in such scenario. Even setting aside practicality of two sets of tables, the chance of getting the calculation wrong or not fast enough is too high.

So none of the methods so far is acceptable. It does not appear possible to have your cake and eat it, too. Yet there is light at the end of the tunnel. Read on.

And now folks, a special edition of the 2I2R for unfortunate owners of scopes with clicks graduated in ¼MOA. (Many of my good friends fell victims of this perversion; US manufacturers of [otherwise excellent] scopes seem to love this.)

Improved Rifleman's rule:
1. Measure the inclination α;
2. Measure the slant distance (along LOS) D;
3. Look up bullet path (come-up) in ballistic table as if shooting at distance D horizontally;
4. Multiply this correction by cos(α).

The secret ingredient, 2I2R-MOA:
5. Subtract one click per each five degrees of inclination over twenty, i.e., 25º -1 click, 30º -2 clicks, 35º -3 clicks, etc.

Results for three different calibres, for the price of one -- check it out:

GP11 2I2R-MOA vertical miss distance, cm

GP90 2I2R-MOA vertical miss distance, cm

.338LM 2I2R-MOA vertical miss distance, cm

Is it not terrific?